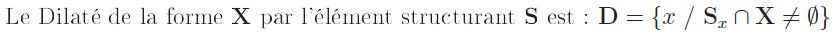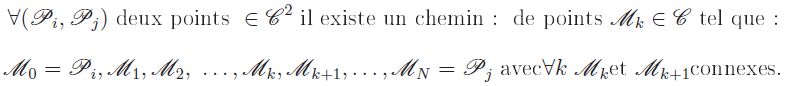I. Introduction▲
L'intérêt de cet article, dont l'objectif est la présentation d'une chaîne simple, mais complète de segmentation, n'est pas uniquement pédagogique. En effet, il est également d'un intérêt pratique, car une telle chaîne de segmentation est généralement rapide ou peu exigeante en termes de puissance de calculs. Ainsi, elle peut être implantée sur un matériel restreint ou classique et fonctionner à la cadence vidéo pour des applications de contrôle qualité en fin de chaîne de fabrication industrielle, de vidéosurveillance, ou même de robotique mobile et autonome telle que l'application RoboCup qui est pour nous très importante.
La constitution d'une telle chaîne simple de segmentation est la suivante :
- une première procédure de sélection rapide des pixels d'intérêt à base de seuillage, suivie éventuellement d'une procédure de filtrage rapide également à partir d'opérateurs agissant sur image binaire. Ces deux procédures sont dites de Bas Niveau : elles admettent en entrée et en sortie une image.
-
une procédure de Niveau Intermédiaire dont le but est de regrouper en taches (la terminologie anglo-saxonne est « Blob Detection ») les pixels d'intérêt de manière à obtenir une information numérique plus globale telle que :
- le centre de gravité,
- la surface,
- la boîte englobante, etc. ;
-
une procédure de Haut Niveau dont l'objectif est de décider :
- la pièce est conforme,
- un intrus a été détecté,
- l'objet recherché dans la scène est trouvé : telle que la balle à suivre pour l'application RoboCup.
II. Seuillages▲
II-A. Principe▲
Le Seuillage consiste à sélectionner ou à classifier certains pixels de l'image, en fonction de la valeur de leur intensité. Le seuillage est un algorithme dit de Bas Niveau :
- l'entrée est une image en niveau de gris ou en couleur pour l'extension à la Classification Couleur ;
- la sortie est une image binaire (i.e. deux niveaux : "0" et "1"), multiniveau (i.e. "0", "1", "2" par exemple pour trois niveaux), ou thématique (i.e. rouge, jaune, bleu, vert, etc., pour une classification couleur).
Le seuillage est constitué par (cf. Article II) :
- le balayage vidéo de la totalité de l'image ;
- et le traitement du pixel courant.
L'algorithme de seuillage nécessite une ou plusieurs valeurs de référence (ou paramètres de contrôle), pour la partie Traitement du Pixel Courant, permettant la sélection ou la classification des pixels.
Il n'y a pas un, mais plusieurs types de seuillages. La figure n° 1 présente la formulation mathématique appliquée pour le traitement du pixel courant pour trois algorithmes différents de seuillage : « classique », « Hat », et « multiple ».
II-B. Seuillage « classique »▲
C'est l'algorithme le plus simple. La formulation mathématique représentant les traitements du pixel courant est représentée figure n° 1, à gauche. Elle consiste à sélectionner un pixel si et seulement si son intensité est supérieure ou égale à la valeur du seuil S :
B(x,y) = "1" si et seulement si I(x,y) >= S
B(x,y) = "0" sinon
où I(x,y) est l'image à seuiller, et B(x,y) l'image seuillée résultat.L'algorithme correspondant au traitement du pixel courant est présenté ci-dessous. Pour visualiser l'image résultat comme une image classique N&B ou en niveaux de gris, l'état "0" sera codé 0 ou noir, et l'état "1" sera codé 255 ou blanc.
* Si I(x,y) >= S
° B(x,y) = "1"
* Sinon
° B(x,y) = "0"II-C. Seuillage « Hat »▲
L'algorithme du seuillage Hat n'est guère plus complexe. La formulation mathématique représentant le traitement du pixel courant est représentée figure n° 1, au centre. Elle consiste à sélectionner un pixel si et seulement si son intensité est comprise entre deux valeurs de seuil :
- bas (low) : SL ;
- et haut (high) :SH .
- B(x,y) = "1" si et seulement si :SL <= I(x,y) <= SH
- B(x,y) = "0"
où I(x,y) est l'image à seuiller, et B(x,y) l'image seuillée résultat.L'algorithme correspondant au traitement du pixel courant est présenté ci-dessous :
* Si SL <= I(x,y) <= SH
° B(x,y) = "1"
* Sinon
° B(x,y) = "0"II-D. Multiseuillage▲
Le Multiseuillage peut être vu comme une généralisation du seuillage Hat. La formulation mathématique représentant le traitement du pixel courant est représentée figure n° 1, à droite. Elle consiste à donner un niveau à tous les pixels en fonction de leur intensité. Le nombre de niveaux pris en compte, c'est-à-dire le nombre de valeurs de seuils S1, S2, S3, ... , Sn dépend du nombre de classes à rechercher. L'algorithme correspondant à la formulation mathématique de la figure n° 1 à droite comporte quatre valeurs de seuils : de S1 à S4, et donc cinq classes :
B(x,y) = "0" si et seulement si I(x,y)< S1,
B(x,y) = "1" si et seulement si S1 <= I(x,y) < S2,
B(x,y) = "2" si et seulement si S2 <= I(x,y) < S3,
B(x,y) = "3" si et seulement si S3 <= I(x,y) < S4,
B(x,y) = "4" si et seulement si S4 <= I(x,y)
où I(x,y) est l'image à seuiller, et B(x,y) l'image seuillée résultat.L'algorithme correspondant au traitement du pixel courant est présenté ci-dessous :
* Si I(x,y) < S1
° B(x,y) = "0"
* Sinon Si S1 <= I(x,y) < S2
° B(x,y) = "1"
* Sinon Si S2 <= I(x,y) < S3
° B(x,y) = "2"
* Sinon Si S3 <= I(x,y) < S4
° B(x,y) = "3"
* Sinon
° B(x,y) = "4"Comme précédemment, pour être visualisables à l'intérieur d'image classique N&B, les états compris entre "0" et "4" sont codés par des valeurs comprises entre 0 et 255, par exemple : 0, 50, 110, 180, et 255.
Un certain nombre d'exercices corrigés ou non et de codes source sont présentés dans parties II (exercices et algorithmies) et III (programmation) de l'ouvrage « Les Bases du Traitement et de la Vision Industrielle et Robotique ». Ils ont fait l'objet de nombreux sujets de partiels.
Les seuillages classique, Hat, multiple et la classification parallélépipédique couleur sont obtenus respectivement par les commandes EdClassicThreshold, EdHatThreshold, EdMultipleThreshold et EdColorClassification. Les codes source des interfaces sont contenus respectivement dans les fichiers EdClassicThreshold.c, EdHatThreshold.c, EdMultipleThreshold.c et EdColorClassification.c. Les codes source des opérateurs sont contenus dans le fichier EdLibThreshold.c. Ces fichiers sont disponibles sur le site web www.developpez.com.
II-E. Résultats et conditions d'utilisation, application▲
Les résultats des seuillages classique, Hat et multiple sont présentés sur l'image du sécateur, figure n° 2 (a). Pour le seuillage classique (b) l'ensemble du sécateur est extrait du fond. La valeur du seuil S est 23. Pour le seuillage Hat (c), seules les deux poignées sont extraites. Les valeurs des seuils S1 et S2 sont respectivement 150 et 210. Pour le multiseuillage (d) trois valeurs de seuils ont été utilisées permettant d'extraire le ressort, les poignées et les lames du fond, éléments classés par ordre d'importance de la valeur de leur intensité. Ces valeurs sont respectivement : 23, 150 et 210(1).
On remarque que le seuillage classique a bien détouré le sécateur, et que le multiseuillage a relativement bien extrait chacune des pièces le composant : ressort, lames et poignées.
On remarque également que le seuillage hat a sélectionné en plus des pixels des poignées, des pixels du bord des lames, c'est-à-dire de la transition entre le fond plus foncé et les lames plus claires. Ces pixels seront filtrés, c'est-à-dire tout simplement supprimés par les opérateurs de traitement sur images binaires, présentés au paragraphe « Traitements sur images binaires », appliqués ensuite.
Le seuillage Hat peut être vu comme la différence entre deux images résultats :
- la première obtenue avec seuil bas ;
- la seconde obtenue avec le seuil haut.
La figure n° 3 illustre ce propos en présentant (a) l'image du bureau, (b) l'image seuillée avec un seuillage Hat, de valeurs de seuil 50 et 70, (c) et (d) l'image seuillée avec un seuillage classique de valeurs de seuil respectives 50 et 70.
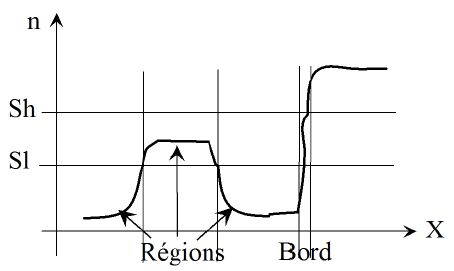
Comme le détaille la figure n° 4, le seuillage Hat sélectionne deux types de pixels (ce que nous avions remarqué figures n° 2 (c) et n° 3 (b)) :
- ceux qui appartiennent à une zone dont les pixels ont des intensités comprises entre les valeurs des seuils bas et haut, c'est par exemple la face avant du bureau de la figure n° 3 (b) ;
- ceux du pourtour(2) d'une zone dont les pixels ont des intensités supérieures au seuil haut et avec un fond dont l'intensité est inférieure au seuil bas. C'est une zone de transition entre régions.
Ce second type de points est généralement indésirable, car n'appartenant pas à un objet proprement dit. Ces points seront filtrés par la suite, par érosion (et ouverture) comme nous le verrons plus loin.
Pour les seuillages classique et Hat, remarquons que les résultats obtenus sont satisfaisants à deux conditions :
- le contenu sémantique de l'image est binaire : il y a les pixels qui sont intéressants et les autres, par exemple le fond ;
- le contenu sémantique se reflète dans la photométrie : les pixels qui nous intéressent se distinguent des autres par leur niveau de gris.
Le choix de l'algorithme de seuillage est le suivant :
- pour le seuillage classique : les pixels intéressants sont les plus clairs (ou les plus foncés à une inversion vidéo près) ;
- pour le seuillage Hat : les pixels intéressants sont de niveaux intermédiaires, ils ne sont ni les plus clairs, ni les plus foncés.
L'image d'un char a bien un contenu sémantique binaire : l'objet d'intérêt (le char ou autre véhicule militaire) et le fond (herbe, arbres ou rochers, etc.). En imagerie N&B ou couleur, le char étant « camouflé », il est impossible par seuillage d'extraire le vert de l'objet sur un fond vert, même en couleur. Le contenu sémantique binaire de la scène n'étant pas reflété dans la photométrie, la seconde condition n'est donc pas validée.
En revanche, en imagerie infrarouge thermique, le char ou le véhicule sont plus chauds que le fond. Il est donc possible de les extraire par simple seuillage, cf. figure n° 5. Remarquons la chaleur plus importante du moteur à l'arrière et également des galets guidant les chenilles.
Le seuillage classique ne permet pas d'extraire uniquement les poignées du sécateur, qui sont d'un niveau de gris intermédiaire entre le fond, plus foncé, d'une part, et les lames, plus claires, d'autre part. En effet, il permet d'obtenir :
- soit le sécateur dans sa globalité (i.e. poignées et lames) ;
- soit les lames seules.
En revanche, le seuillage Hat le permet (cf. figure n° 2 (c)).
Seuiller l'image du bureau n'a pas d'intérêt pratique. En revanche, les formes obtenues ont un intérêt pédagogique pour visualiser l'effet des opérateurs de morphologie mathématique présentés ensuite.
Pour le seuillage multiple, diverses catégories de pixels sont intéressantes, et se caractérisent également par leurs différentes plages de niveaux de gris.
II-F. Utilisation de l'histogramme ▲
L'histogramme est d'un grand secours pour la détermination du ou des seuils, qu'elle soit manuelle (par un opérateur humain) ou automatique, c'est-à-dire sans aucun réglage externe.
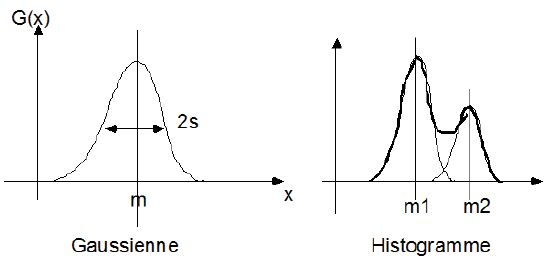
Un objet, homogène à l'œil dans l'image, ne se traduit généralement pas par un niveau de gris unique, représenté par une raie unique dans l'histogramme. Il se traduit par une répartition « en cloche » modélisée par une répartition gaussienne autour d'une valeur moyenne (cf. figure n° 6, à gauche). Lorsque l'image représente un objet sur un fond, en supposant l'objet et le fond sont homogènes, l'histogramme est alors constitué de deux répartitions en cloche. On parle alors d'histogramme bimodal (cf. figure n° 6, à droite). La valeur du seuil doit être choisie de manière à séparer les deux modes, l'un représentant le fond, l'autre l'objet recherché.
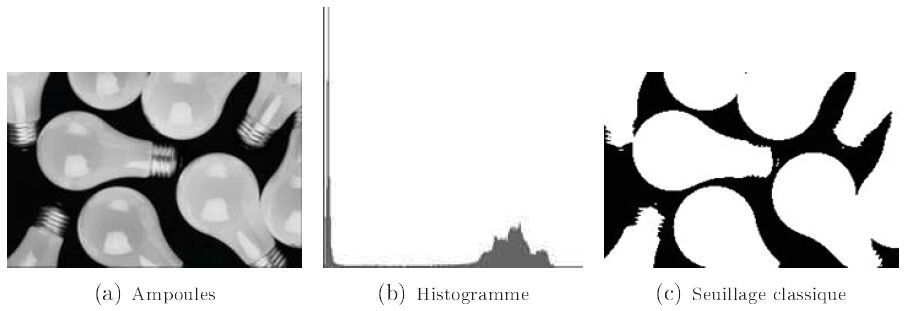
L'image des ampoules de la figure n° 7 illustre ce propos. Son histogramme est bimodal. Le mode foncé représente le fond, le mode clair les ampoules. Les deux modes sont bien séparés, ce qui veut dire que le choix de la valeur du seuil n'est pas critique : un certain nombre de valeurs différentes donnent des résultats quasi identiques.
Il existe des histogrammes plus complexes : tri-, quadri-... , modal. On comprend ainsi l'intérêt du seuillage Hat qui permet d'isoler l'un des modes, ainsi que du multiseuillage qui permet d'affecter un niveau par mode de l'histogramme.
Ce cas idéal n'arrive malheureusement pas tout le temps. Observons l'histogramme de l'image du sécateur, figure n° 8 (a), en visualisation linéaire (b). On distingue un énorme « pic » lié aux nombreux pixels du fond et on imagine, car ils sont minuscules deux pics plus clairs :
- le premier, de niveaux de gris intermédiaires correspondant aux deux poignées ;
- le second plus clair, correspondant aux lames.
C'est un histogramme trimodal.
Pour la visualisation, la Normalisation Linéaire d'équation :
visu[n] = histo [n] * 255 / maxi
où maxi est le maximum de l'histogramme, ayant une valeur importante écrase les autres valeurs. En revanche, la Normalisation Logarithmique (cf. figure n° 8 (c)) d'équation :
visu[n] = log(1 + histo [n]) * 255 / log (1+ maxi)
permet la visualisation de ces deux pics, mais est bien plus bruitée.
Les valeurs des seuils peuvent être obtenues à partir de l'histogramme de l'image par un opérateur humain. Mais dans certaines applications, automatiques, le recours à un opérateur humain est impossible. Les valeurs des seuils doivent être déterminées automatiquement. Pour ce faire, certains traitements peuvent être effectués sur l'histogramme afin de le lisser. De même, il peut exister un certain nombre de minima ou de maxima locaux perturbant la détermination des seuils. Ces traitements, hors du champ d'investigation de cette première série d'articles présentant des bases, seront présentés lors d'une seconde série.
II-G. Classification couleur RVB▲
Une zone d'une couleur quelconque en imagerie RVB est comme une zone homogène en imagerie N&B, sauf que l'homogénéité se retrouve sur les trois composantes R,V et B. La répartition des intensités des pixels n'est plus exactement autour d'une valeur moyenne à une dimension, mais autour d'un point de l'espace 3D RVB, soit un nuage de points. Ce nuage de points va être approximé par le volume du parallélépipède rectangle l'englobant dans l'espace 3D RVB. Ainsi, il est donc très simple de passer du Seuillage Hat en imagerie N&B au Classifieur Couleur Parallélépipédique en imagerie couleur RVB, en effectuant un seuillage Hat par composante comme cela va être montré ci-dessous.
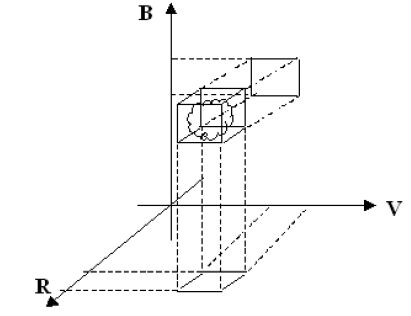
Pour retenir un pixel comme appartenant à une couleur définie a priori, le classifieur couleur parallélépipédique vérifie que les trois composantes R,V,B du pixel à classifier appartiennent aux bonnes plages sur les trois axes RVB comprises entre Rmin et Rmax, Vmin et Vmax, Bmin et Bmax, c'est-à-dire :
(Rmin ≤ R ≤ Rmax) ET (V min ≤ V ≤ Vmax) ET (B min ≤ B ≤ Bmax)
comme schématisé figure n° 9.
Le test permettant de déterminer si un pixel couleur est d'une couleur de référence donnée, comporte uniquement un seuillage Hat par composante. Ainsi, six comparaisons seulement sont nécessaires pour savoir si un pixel couleur est d'une couleur référencée.
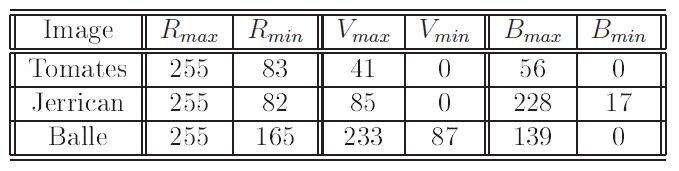
Des exemples de résultats obtenus par ce classifieur sont présentés figure n° 10 sur l'extraction de pixels « rouges » correspondant à des tomates, « roses » correspondant à un jerrican et « oranges » correspondant à la balle pour l'application RoboCup. Les valeurs respectives des seuils : Rmax, Rmin, Vmax, Vmin, Bmax, Bmin sont présentées tableau ci -dessous.
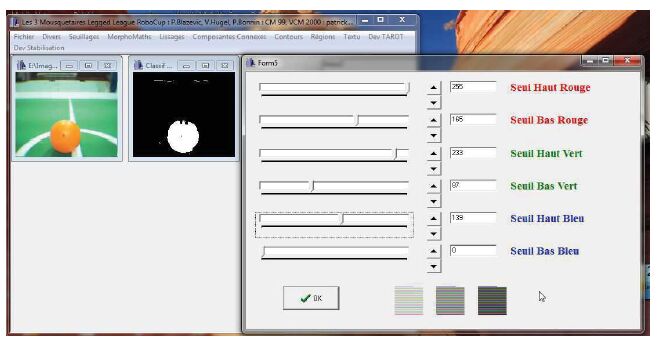
Les valeurs des seuils Rmax, Rmin, Vmax, Vmin, Bmax, Bmin,paramètres de la classification couleur parallélépipédique peuvent être déterminées en « tâtonnant » en utilisant le programme PcolorClassification fourni dans la bibliothèque logicielle EdVision. Mais cette sélection risque d'être fastidieuse. Il est préférable de disposer d'une interface graphique, telle que celle que nous avons programmée pour des besoins en enseignement, présentée figure n° 11, où le calcul de la classification est réeffectué en temps réel à chaque modification par les réglettes et/ou les boutons up/down des valeurs des paramètres.
Les résultats obtenus, cf. figure n° 10, présentent les mêmes caractéristiques que ceux du Seuillage Hat(3). En effet, en plus des pixels appartenant à l'objet désiré, des pixels appartenant à des zones de transition sont également sélectionnés. Ces pixels seront éliminés par les mêmes traitements sur image binaire que pour le seuillage Hat.
Avis personnel en conclusion
Ces méthodes sont très efficaces, et très rapides lorsqu'elles peuvent être appliquées. Malheureusement, leur domaine d'application est très restreint : notamment au niveau des conditions d'éclairage qui doivent rigoureusement être invariantes, sinon les paramètres de seuillages ne sont plus correctement réglés.
SONY a proposé un classifieur couleur, intégré en matériel dans son robot AIBO. Ce classifieur, bien plus complexe est appliqué dans l'espace colorimétrique YUV. Chaque couleur est définie par 128 paramètres. Nous présenterons ce classifieur dans un article de la seconde série.
III. Traitement sur images binaires▲
Ces traitements sont nécessaires pour filtrer les points indésirables sélectionnés par les seuillages précédents, ou pour trouver certains points particuliers, centres de formes particulières : bord, coin, point isolé, etc.
Ils peuvent être classifiés en deux catégories :
- ceux qui peuvent être modélisés mathématiquement à l'aide de la théorie des ensembles et de la topologie : la Morphologie Mathématique sur images binaires ;
- les autres.
III-A. Morphologie mathématique sur images binaires▲
Nous allons présenter les quatre opérateurs de base suivants :
- « Érosion » ;
- « Dilatation » ;
- « Ouverture » et « Fermeture » qui sont des combinaisons des opérateurs d'érosion et de dilatation.
III-A-1. Enseignement classique▲
L'enseignement classique de l'opérateur d'érosion issu de l'Annexe C de l'excellent ouvrage de référence (4) est le suivant
III-A-2. Un peu de pédagogie▲
La formulation précédente, belle mathématiquement est loin d'être compréhensible par un étudiant à BAC + 2 d'une formation de type DUT GEII, GIM, GMP, MP, R&T, Informatique ou autre ! Ainsi, nous n'enseignerons pas la Morphologie Mathématique ici de manière classique. Cette manière nous est parfaitement personnelle.
Ces deux cas simples, de l'érosion et de la dilatation, nous permettent d'aller plus loin pédagogiquement. Comment concevoir un algorithme en partant du cahier des charges : i.e. de l'effet visuel escompté, ce de manière pragmatique.
Nous ne donnons pas l'algorithme comme nous l'avons fait jusqu'à présent. Ici nous allons le déduire ensemble !
Cette méthode est bien évidemment à réutiliser, dans des cadres plus complexes, tels que pour la conception d'algorithmes permettant une segmentation en contours ou en régions. Partant du cahier des charges, une solution au problème peut être trouvée à partir de dessins.
III-A-3. Érosion▲
Principe
L'érosion consiste à enlever un pixel tout autour de la forme.
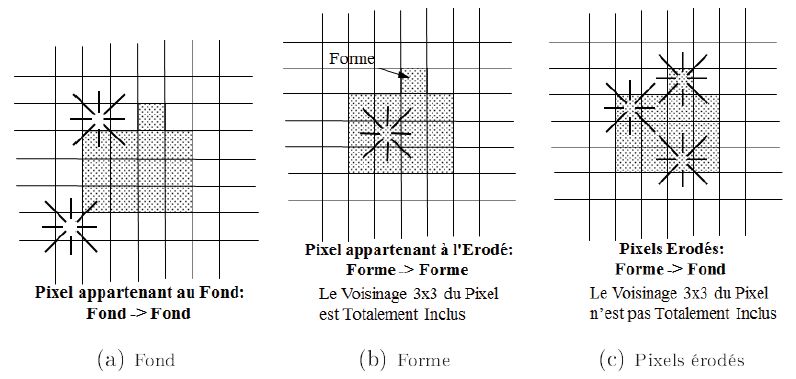
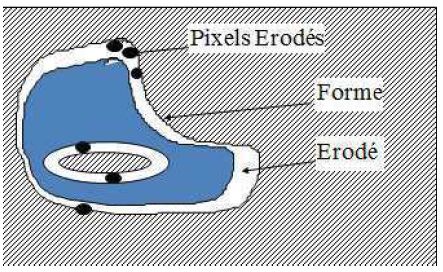
Autour signifie aussi bien sur le Pourtour(5) externe (c'est-à-dire extérieur de la forme) qu'interne pour une forme ayant des trous. Il y a trois types de pixels (cf. figure n° 12) :
- les pixels du fond : aussi bien dans l'image initiale, que dans l'image érodée :
- les pixels de l'érodé : ils appartiennent à la forme dans l'image originale et à l'érode (c'est-à-dire la nouvelle forme) dans l'image érodée ;
- les pixels érodés : ce sont les pixels du pourtour, ils appartiennent à la forme dans l'image initiale, et au fond dans l'image érodée.
Du cahier des charges à l'algorithme
Les pixels des deux premières catégories : du fond et de l'érodé ne changent pas d'état au cours de l'érosion : ils sont respectivement fond et forme et ils le restent. En revanche les pixels érodés changent d'état : ils passent de la forme au fond.
Dessinons une forme(6) et caractérisons les trois types de pixels précédents. Les plus simples sont les pixels du fond figure n° 13 (a), qui restent fond par érosion. Comment différencier les pixels érodés, c'est-à-dire ceux qui vont changer d'état, des pixels de l'érodé qui vont rester forme ?
Les pixels érodés sont au bord de la forme, alors que les pixels de l'érodé sont à l'intérieur de la forme. Cette différence est mise en évidence lors de l'examen du voisinage 3 x 3 centré du pixel courant. En effet, être à l'intérieur de la forme signifie que le voisinage 3 x 3 centré du pixel courant est totalement inclus dans la forme, cf. figure n° 13 (b). Alors qu'être au bord de la forme signifie que ce voisinage inclut des pixels de fond, cf. figure n° 13 (c).
Ainsi nous allons proposer deux manières complètement similaires et aussi simples l'une que l'autre de répondre au cahier des charges :
- première méthode : par détection des pixels de l'érodé, la plus intuitive ;
- seconde méthode : de recopier l'image en détectant les pixels érodés qui changent d'état.
Pour chacune de ces deux méthodes, il faut examiner le pixel courant et son voisinage 3 x 3 centré :
- pour un pixel de l'érodé : le pixel central appartient à la forme, ainsi que tout son voisinage ;
- pour un pixel érodé : le pixel central appartient à la forme, et son voisinage contient des pixels du fond.
Premier algorithme
Un premier algorithme simple satisfaisant aux deux méthodes est le suivant : il s'agit de calculer un ET LOGIQUE sur l'ensemble des pixels du voisinage 3 x 3 centré. Le résultat obtenu est le suivant :
- état "1" ou Є à la forme pour les pixels de l'érodé ;
- état "0" ou à la forme pour les pixels du fond, et érodés.
L'inconvénient de ce premier algorithme est que de faire un ET LOGIQUE sur le voisinage 3 x 3 centré de chaque pixel, prend du temps ou de la puissance de calcul, alors que cette opération n'est obligatoire que sur les pixels de la forme, peu nombreux dans l'image dans la plupart des applications, notamment militaires où l'on recherche de petites cibles.
Nous proposons donc un second algorithme, satisfaisant également aux deux méthodes.
Second algorithme (7)
Les deux caractéristiques d'un pixel de l'érodé (respectivement érodé) sont les suivantes :
- le pixel courant appartient à la forme dans l'image originale ;
- son voisinage 3 x 3 centré appartient totalement à la forme (respectivement il existe un pixel de fond dans son voisinage).
Les résultats comparés des quatre opérateurs de morphologie mathématique présentés : érosion, dilatation, ouverture et fermeture sont présentés plus loin dans cet article.
III-A-4. Dilatation▲
Note
Compte tenu de la similarité entre les opérateurs d'érosion et de dilatation,nous allons reprendre la même présentation. Nous en déduirons, à la fin, une analogie pratique.
Principe
La dilatation consiste à ajouter un pixel tout autour de la forme.
Ce principe est bien plus compréhensible que la formulation mathématique de l'annexe C de l'excellent ouvrage de référence :
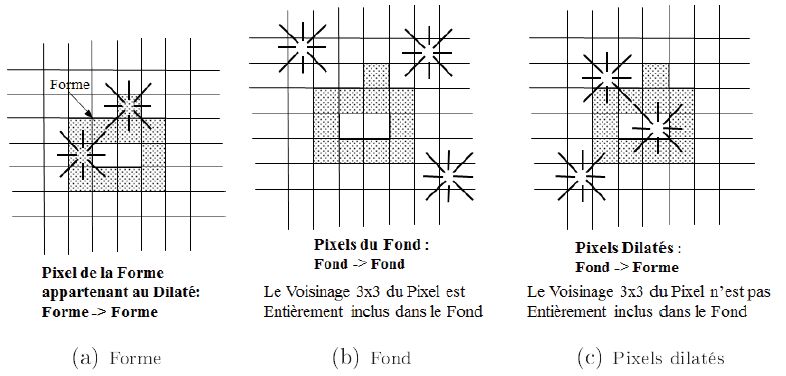
Il y a trois types de pixels (cf. figure n° 14) :
- les pixels de la forme : aussi bien dans l'image initiale, que dans l'image dilatée où ils appartiennent au Dilaté, c'est-à-dire à la nouvelle forme ;
- les pixels « de l'intérieur » du fond : ils appartiennent simultanément au fond dans l'image originale et dans l'image dilatée ;
- les pixels dilatés : ils appartiennent au fond dans l'image initiale, et à la forme ou au dilaté dans l'image dilatée.
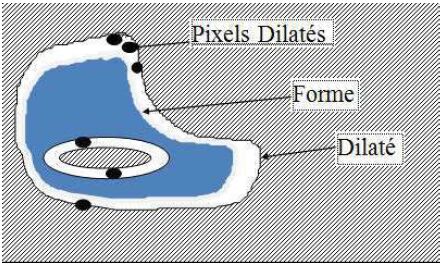
Du cahier des charges à l'algorithme :
Les pixels des deux premières catégories : de la forme et de l'intérieur du fond ne changent pas d'état au cours de la dilatation : ils sont respectivement forme et fond et ils le restent. En revanche les pixels dilatés changent d'état : ils passent du fond à la forme.
Comme pour l'érosion, en dessinant une forme, caractérisons les trois types de pixels précédents. Les plus simples sont les pixels de la forme figure n° 15 (a) qui restent forme par dilatation. Comment différencier les pixels dilatés, c'est-à-dire ceux qui vont changer d'état, des pixels de l'intérieur du fond qui vont rester fond ?
Les pixels dilatés sont au bord du fond, alors que les autres sont à l'intérieur du fond. Cette différence est en évidence lors de l'examen du voisinage 3 x 3 centré du pixel courant. En effet, être à l'intérieur du fond signifie que le voisinage 3 x 3 centré du pixel courant est totalement inclus dans fond, cf. figure n° 15 (b). Alors qu'être au bord du fond signifie que ce voisinage inclut des pixels de la forme, cf. figure n° 15 (c).
Comme pour l'érosion, nous allons proposer deux manières complètement similaires et aussi simples l'une que l'autre de répondre au cahier des charges :
- première méthode : par détection des pixels de l'intérieur du fond, c'est-à-dire du complémentaire(8) du dilaté ;
- seconde méthode : de recopier l'image en détectant les pixels dilatés qui changent d'état.
Pour chacune des deux méthodes, il faut examiner le pixel courant et son voisinage 3 x 3 centré :
- pour un pixel de l'intérieur du fond : le pixel central appartient au fond, ainsi que tout son voisinage ;
- pour un pixel dilaté : le pixel central appartient au fond, et son voisinage contient des pixels de la forme.
Premier algorithme
Comme pour l'érosion, un premier algorithme simple satisfaisant aux deux méthodes est le suivant : il s'agit de calculer un OU LOGIQUE sur l'ensemble des pixels du voisinage 3 x centré. Le résultat obtenu est le suivant :
- état "1" ou Є à la forme pour les pixels du dilaté ;
- état "0" ou Є au fond pour les pixels de l'intérieur du fond.
Ainsi pour passer de l'érosion à la dilatation, on remplace l'opérateur ET LOGIQUE par l'opérateur OU LOGIQUE, qui conserve le même inconvénient au niveau du temps ou de la puissance de calcul nécessaire. Nous proposons donc un second algorithme, satisfaisant également aux deux méthodes.
Second algorithme
Les deux caractéristiques d'un pixel de l'intérieur du fond (respectivement dilaté) sont les suivantes :
- le pixel courant appartient au fond dans l'image originale ;
- son voisinage 3 x 3 centré appartient totalement au fond (respectivement il existe un pixel de la forme dans son voisinage).
Les résultats de la dilatation seront comparés à ceux des trois autres opérateurs plus tard dans cet article.
Dualité : Érosion - Dilatation
La forme et le fond sont deux espaces complémentaires, i.e. :
la forme U le fond = l'image.
Ainsi on remarque qu'éroder la forme, c'est-à-dire lui enlever un pixel tout autour, revient à dilater le fond : c'est-à-dire lui ajouter un pixel tout autour. Réciproquement, dilater la forme revient à éroder le fond. Cette propriété prend le nom de Dualité entre l'érosion et la Dilatation.
Nous présentons dans la partie II (Algorithmie et Exercices) et III (Programmation) de notre ouvrage, la conséquence de cette propriété. En effet, le second algorithme de la dilatation par détection des pixels dilatés s'obtient simplement à partir du second algorithme de l'érosion par la détection des pixels érodes en inversant les tests sur le pixel courant et les pixels voisins, ainsi que les actions de mise à l'état "1" ou "0".
III-A-5. Ouverture et fermeture▲
L'ouverture et la fermeture sont des combinaisons des opérateurs d'érosion et de dilatation.
Principe de l'ouverture :
L'ouverture consiste à effectuer une érosion, suivie d'une dilatation.
Cette combinaison est elle l'opérateur identité ? Réponse ci-dessous.
Principe de la fermeture
La fermeture, combinaison inverse de l'ouverture consiste à effectuer une dilatation, suivie d'une érosion.
Même question que pour l'ouverture.
Propriété d'idempotence
La propriété d'idempotence pour une fonction f est : f o f= f
Les opérateurs d'ouverture d'une part, et de fermeture d'autre part sont idempotents. Ceci signifie que de faire deux ouvertures (respectivement fermetures), à la suite l'une de l'autre, revient à en faire une seule. La raison sera expliquée lors de la présentation des résultats.
En mathématiques, la projection orthogonale dans une direction donnée est une fonction idempotente.
Les opérateurs d'érosion, de dilatation, d'ouverture et de fermeture sont obtenus respectivement par les commandes EdErosion, EdDilation, EdOpening et EdClosing. Les codes source des interfaces sont contenus dans les fichiers EdErosion.c, EdDilation.c, EdOpening.c et EdClosing. Les codes source des opérateurs sont contenus dans le fichier EdLibBinaryMorphoMath.c.
III-A-5-a. Résultats▲
Les résultats comparés des quatre opérateurs : érosion, dilatation, ouverture et fermeture sont présentés sur l'image du bureau seuillée figure n° 16.

L'érosion (cf. résultats figure n° 16 (b)) enlève bien un pixel tout autour de la forme : à l'extérieur aussi bien qu'à l'intérieur. Ceci a pour effet notamment de supprimer tous les petits détails de la forme. Un petit détail est caractérisé par le fait qu'il ne contient pas un carré de taille 3 x 3. Ainsi, les détails ponctuels ont disparu, ainsi que les détails filaires ou filiformes comme une partie des barreaux horizontaux des fenêtres.
La dilatation (cf. résultats figure n° 16 (c)) ajoute bien un pixel tout autour de la forme : à l'extérieur aussi bien qu'à l'intérieur. Ceci revient à diminuer d'un pixel le fond et a pour effet notamment de supprimer tous les petits détails du fond : ponctuels ou filiforme. Ainsi, la dilatation bouche les trous de la forme (cf. le trou en bas de la face avant du bureau).
L'ouverture, composée d'une érosion suivie d'une dilatation enlève un pixel, puis rajoute un pixel tout autour de la forme. Retombe-t-on sur l'image originale ? La réponse est bien évidemment NON, sinon cet opérateur n'aurait pas d'intérêt. Examinons en détail son comportement (cf. résultats figure n° »16 (d)) :
- les formes de taille importante : perdent un pixel, puis le regagnent. Elles ne changent globalement pas, à très peu de pixels près ;
- les détails ponctuels ou filiformes : ils disparaissent totalement après l'érosion, donc la dilatation n'aura aucun effet sur eux.
Ainsi l'ouverture a pour effet :
- de laisser quasi identiques les formes de taille importante ;
- de supprimer les détails ponctuels ou filiformes.
Cet effet est particulièrement recherché après un seuillage, où le bruit de détection (i.e. l'imperfection) se traduit par de tels détails. Par exemple sur l'image (d), certains montants des fenêtres ont disparu.
Plus concrètement, l'ouverture permet de filtrer les points du pourtour d'une forme dont l'intensité est supérieure au seuil haut, comme le pourtour des lames du sécateur figure n° 2.
La fermeture (cf. résultats figure n° 16 (e)) produit un effet similaire à l'ouverture, mais pour le fond, c'est-à-dire pour les trous de la forme. Ainsi, la dilatation va boucher les trous ponctuels ou filiformes de la forme, que l'érosion ne débouchera pas.
Sur une même image, il est possible d'employer une ouverture, puis une fermeture si l'on a besoin des deux effets.
Retour sur l'idempotence de l'ouverture et de la fermeture
Pour la première ouverture :
- lors de l'érosion, les objets de taille importante ont perdu un pixel tout autour, et les détails ponctuels ou filiformes ont disparu ;
- lors de la dilatation, les objets de taille importante reprennent (à quelques pixels près) leur forme initiale. Il ne reste plus qu'eux.
Pour la seconde ouverture :
- lors de l'érosion, les objets de taille importante perdent le pixel tout autour de la forme qui a été remis lors de la précédente dilatation, donc reprennent la forme d'après l'érosion de la première ouverture ;
- la dilatation leur remet le pixel tout autour : ils reprennent leur aspect d'après la première ouverture. D'où l'idempotence.
Il en est de même pour la fermeture, en remplaçant détail de la forme par détail du fond, donc petit trou de la forme.
III-B. Autres traitements▲
Pour certaines applications(9) il est nécessaire de repérer, dans une image binaire, les points qui sont localement (i.e. dans leur voisinage 3 x 3 centré, cf figure n° 17) : des Bords, ou des Coins des formes.
Ces traitements se prêtent moins bien à une formalisation mathématique. En revanche, passer du cahier des charges (i.e. de la forme du point recherché) à l'algorithme n'est pas plus complexe. Nous en proposons un algorithme et le détail du code source correspondant dans notre ouvrage.
III-C. Adaptation au multiniveau▲
Il s'agit d'adapter les traitements précédents : d'érosion, de dilatation, et de recherche de points de bords ou de coins dans le cas d'une image multiniveau.
L'adaptation des opérateurs d'érosion et de recherche de points de bords ou de coins est la plus simple. En effet, pour la recherche de points de bords ou de coins : il est possible de reprendre l'algorithme en imagerie binaire en considérant comme point appartenant à la forme, uniquement les points du niveau considéré, c'est-à-dire du niveau du pixel central. Les autres niveaux, ainsi que le fond sont considérés comme fond.
Pour l'opérateur d'érosion en multiniveau, les pixels érodés qui seront mis à l'état « Fond » à l'issue de l'érosion possèdent les caractéristiques suivantes :
- ce sont des pixels d'un niveau donné ;
- qui possèdent dans leur voisinage 3 x 3 centré au moins un pixel soit d'un autre niveau, soit du fond.
L'adaptation de l'opérateur de dilatation n'est guère plus complexe. Un pixel dilaté possède les caractéristiques suivantes :
- c'est un pixel du fond ;
- qui possède dans son voisinage 3 x 3 centré au moins un pixel n'appartenant pas au fond.
Le pixel dilaté prendra le niveau le plus représenté dans son voisinage 3 x 3.
IV. Composantes connexes ou « Blob Detection » ▲
IV-A. Objectif▲
L'objectif est de regrouper les différents pixels voisins(10) de la forme et éventuellement du fond en Composantes Connexes ou Blobs(11). Pour ce faire, il faut affecter une seule et même étiquette (ou label), c'est-à-dire un même nombre à tous les pixels de la composante connexe. Un nombre étant équivalent par table de transcodage à une couleur, on comprend aisément pourquoi ce type d'algorithmes est souvent appelé « Algorithme du Peintre ».
La principale difficulté, comme nous allons le voir, est qu'une même composante connexe va se voir attribuer initialement plusieurs étiquettes, et qu'il va falloir gérer les équivalences entre étiquettes, c'est-à-dire la transitivité. Nous ne rentrerons pas dans les détails de cet algorithme, dans cette première série d'articles, dédié au niveau Bachelor. Nous le ferons dans la suivante.
IV-B. Définition▲
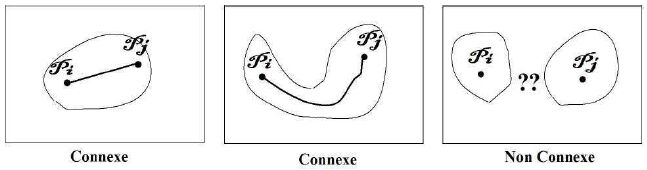
Un ensemble de pixels est une composante connexe C si et seulement si :
Le chemin entre les deux points est quelconque, et non forcément en ligne droite, ce qui assurerait la propriété de Convexité. Ainsi, une zone de l'image en forme de croissant est Connexe (cf. figure n° 18, au centre), mais n'est pas Convexe. En revanche, la forme à droite n'est pas connexe… il y a bien deux taches !
IV-C. Un Exemple : l'algorithme de A. Rosenfeld et J.L. Pfalz▲
Le principe proposé par A. Rosenfeld, J.L. Pfalz, en 1966 comporte les caractéristiques suivantes. L'algorithme comporte deux balayages de l'image. Le premier, permet la propagation des étiquettes (cf. algorithme ci-dessous) en examinant le voisinage passé 4-connexe du pixel courant (masque dit en "L inversé"), et en gérant les incompatibilités d'étiquetage, évoquées ci-dessus, à l'intérieur d'un tableau de transcodage. Le second consiste à appliquer un tableau de transcodage. Il permet de remplacer la valeur de l'étiquette obtenue après le premier balayage, par l'étiquette équivalente de valeur la plus faible.
L'algorithme produit :
- une image des étiquettes où chaque pixel est affecté du numéro de la composante connexe à laquelle il appartient, ou de l'étiquette nulle (0), s'il n'appartient à aucune ;
- une structure de données où sont stockés les attributs (valeurs numériques, voir ci-dessous) de chaque composante.
La « fusion » des composantes connexes, consécutive aux conflits d'étiquetage est gérée au niveau de la structure de données des attributs des composantes connexes.
L'algorithme est le suivant.
* Initialisation : l'étiquette courante 'etq' est initialisée à 1
* Premier balayage vidéo de l'image et pour le point courant :
° Recherche des pixels dans le passé en 4-connexité à même niveau
- Si aucun
> affecter au pixel l'étiquette courante 'etq'
> incrémenter etq d'une unité
- Si un seul
> le pixel courant prend l'étiquette de son voisin (propagation)
- Si deux, mais de même étiquette
> le pixel courant prend l'étiquette de ses voisins (propagation)
- Si deux, mais d'étiquettes incompatibles (différentes)
> affecter le pixel courant de l'étiquette de numéro le plus petit,
> relever l'équivalence entre les étiquettes.
* Second balayage vidéo de l'Image
° Mise à jour de l'étiquette du pixel courantLa figure n° 19 présente les résultats obtenus sur plusieurs images :
- le sécateur : image traitée à l'aide d'un seuillage « Hat » puis d'une ouverture ;
- les ampoules : image traitée à l'aide d'un seuillage « classique » puis d'une ouverture ;
- les tomates : image traitée à l'aide d'une classification couleur parallélépipédique dans l'espace colorimétrique RVB puis d'une ouverture.
Interprétation des résultats
Sur l'image du sécateur : les résultats obtenus par ce traitement très simple sont parfaits : les deux poignées recherchées sont bien trouvées. Nous verrons ci-dessous qu'ils nous permettront de décider si le sécateur est correctement assemblé ou non dans le cadre d'un contrôle qualité en fin de chaîne de fabrication.
Sur l'image des ampoules : le problème est plus complexe, car les ampoules sont collées les unes aux autres. Il est difficile, par conséquent, de les compter simplement.
Sur l'image des tomates : des ombres sont également détectées et les tomates en grappes sont divisées en plusieurs composantes connexes à cause des branches.
V. Filtrage sur attributs▲
V-A. Attributs des composantes connexes▲
Les attributs des composantes connexes sont de deux types :
-
géométriques (cf. figure n° 20) :
- la Surface S,
- le Centre de gravité : (xG, yG),
- la Boîte englobante : xmin, xmax, ymin, ymax ;
-
photométrique, dans le cas de l'imagerie multiniveau :
- le niveau.
V-B. Calcul des attributs▲
Pour la surface S, cet attribut mis à 1 à la création avec le premier pixel, puis incrémenté d'une unité à l'inclusion de chaque pixel.
La boîte englobante est initialisée au premier pixel :
xmin = x, xmax = x, ymin = y, ymax = y,
puis mise à jour à l'inclusion de chaque pixel : par exemple pour xmin et xmax :
* Si xmin > x
- xmin = x
* Sinon Si xmax < x
- xmax = xIl en est de même pour ymin et ymax.
La formule du calcul du centre de gravité est :
Pour ce faire, on va cumuler les abscisses et les ordonnées de chaque pixel inclus, soit :
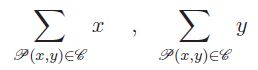
Le calcul du centre de gravité sera effectué à la fin.
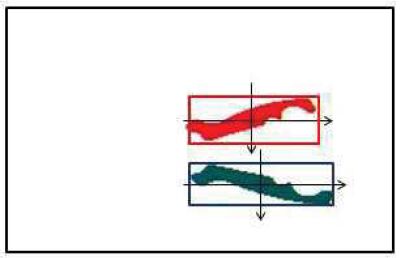
Pour rechercher des objets de forme allongée, la boîte englobante avec des axes parallèles aux axes de l'image (cf. figure n° 20) n'est pas adéquate. En effet, si l'objet est en biais (orientation proche de 45°) la boîte englobante n'est pas représentative de la forme. Il est alors possible de calculer les axes d'inertie de la forme, puis la boîte englobante avec des axes parallèles aux axes d'inertie de l'objet, qui elle l'est (cf. figure n° 21). Mais, les calculs sont bien plus complexes.
V-C. Filtrage sur attributs…▲
Il consiste simplement à rechercher dans l'image des composantes connexes dont les attributs sont dans une certaine plage de tolérance : par exemple pour la surface S :
Smin ≤ S ≤ Smax, ou la taille de la Boîte Englobante :
dx = xmax - xmin + 1 et dy = ymax - ymin + 1
VI. Prise de décision▲
La prise de décision relative à la conformité d'une pièce en contrôle qualité par vision industrielle peut être simple :
- à partir d'un filtrage sur un ou plusieurs attributs ;
- par la détection de trous : nombre, et positionnement corrects ;
-
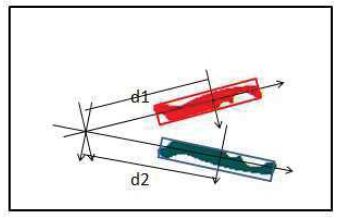
pour le sécateur (cf. figure n° 21) :
- présence des deux manches,
- conformité (filtrage sur attributs) de l'angle entre les deux axes d'inertie,
- conformité des deux distances d1 et d2 entre le point d'intersection deux axes d'inertie et des boîtes englobantes des manches parallèles à ces axes.
VII. Conclusion▲
Dans cet article, le quatrième de la série, nous avons présenté :
- un certain nombre d'opérateurs simples, rapides, très efficaces dans certains contextes applicatifs, permettant de réaliser une première chaîne complète de segmentation, c'est-à-dire une application complète de vision ;
- le contexte précis de l'application dans lequel ces opérateurs doivent être utilisés.
Nous conseillons au lecteur désirant « Apprendre à concevoir et à réaliser des opérateurs de traitement d'image ou de vision » de commencer par ceux-ci. Leur code source est disponible sur le site web du site « Developpez.com », les explications de leur algorithme et de leur code source dans les parties II (Algorithmes et Exercices) et III (Programmation) de notre ouvrage.
L'article suivant, intitulé Segmentation en Contours présente la notion de contour, les différentes étapes constituant une segmentation en contours, puis le principe des trois premières : le calcul du gradient, le seuillage sur la norme du gradient, et l'affinage.